Organisation du système de production Partie 4: Planning de production
Table des Matières
| IUT GON SITE D’ALENÇON | DEPARTEMENT QLIO | BUT S2 |
Élaboration d’un diagramme de PERT#
Représentation sagittale d’un process#
Il peut être utile de cartographier l’implantation d’une ligne de production pour avoir une vue d’ensemble des relations entre les différentes opérations.
On peut utiliser les représentations sagittales1 pour illustrer les suites d’opérations prenant place dans un atelier ou une gamme de production.
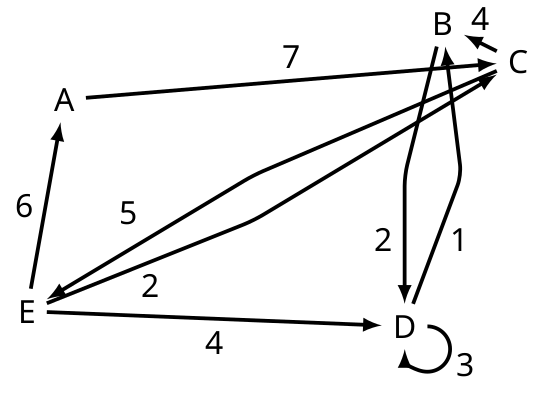
Schéma d’implantation fictive.
Ici, les numéros représentent des longueurs, généralement des distances entre deux opérations ou des temps de transfert.
Quelques notions de vocabulaire des diagrammes sagittaux:
- Arc: Lien entre deux sommet représenté par une flèche.
- Chemin: Un ensemble d’arcs. Par exemple le chemin (ACB)
- Valeur: Numéro associé à chaque arc. La valeur d’un chemin est la somme des valeurs de ses arcs. Pour (ACB), la valeur est égale à $7+4=11$.
- Longueur: Le nombre d’arcs d’un chemin. Pour (ACB) on a deux arcs, (AC) et (CB) donc la longueur du chemin est de 2.
Enfin on parle de boucles fermées lorsqu’un chemin revient sur lui-même. Par exemple (ACEA).
Les diagramme sagittaux peuvent être vite chargés pour représenter un process industriel de manière géographique. Même optimisée, l’implantation d’une usine ne permet pas forcément d’avoir une vue d’ensemble claire de la dépendance des opérations les unes par rapport aux autres.
Un autre moyen de représenter les relations entre des processus est la représentation matricielle. Elle permet de savoir quel opérations sont reliées entre-elles d’un seul coup d’œil:
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | 1 | ||||
| B | 1 | ||||
| C | 1 | 1 | |||
| D | 1 | 1 | |||
| E | 1 | 1 | 1 | 1 |
La représentation PERT2 essaie de proposer une représentation sagittale alternative permettant de déterminer facilement et la dépendance entre les opérations et les contraintes temporelles incompressibles comme les chemins critiques.
Diagrammes de PERT#
Les diagrammes de PERT ne tiennent pas compte des notions de charge ou de capacité mais permettent de déterminer le temps nécessaire pour parcourir un chemin et les chemins critiques de fabrications (ceux qui imposent le temps minimal).
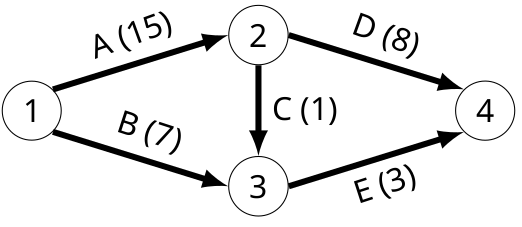
Un exemple simple de diagramme de PERT.
Le diagramme de PERT est une représentation immuable de l’enchaînement des opérations. Mais attention, chaque opération est représentée par un arc et pas par leurs sommet. Les sommet représentent les étapes d’avancement.
Réalisation d’un diagramme de PERT
Préparation des données
Pour réaliser un diagramme de PERT on commence par lister les relations de dépendance entre les opérations concernées. Soit la suite d’opérations suivantes avec leur temps et les opérations dont elles dépendent:
- B = 3/ACEF
- C = 2/A
- D = 8/A
- F = 1/A
- G = 3/ACE
- A = 15
- E = 7
On peut en construire la représentation matricielle suivante:
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| A | 1 | 1 | 1 | 1 | 1 | ||
| B | |||||||
| C | 1 | 1 | |||||
| D | |||||||
| E | 1 | 1 | |||||
| F | 1 | ||||||
| G | |||||||
| rang | 1 | 3 | 2 | 2 | 1 | 2 | 3 |
Pour établir le rang de chaque étape on cherche les colonnes vides (pas de dépendance). Ces dernières seront de rang 1. On supprime ensuite les lignes des colonnes de rang 1. Les nouvelles colonnes vides seront les opérations de rang 2. On supprime les lignes des opérations de rang 2 etc…
À partir de la matrice 2 on cherche à établir un graphe:
- Séquentiel: c’est à dire sans retour ou boucle
- Monographe: c’est à dire avec un seul arc entre chaque sommet
Élaboration du graphique
On place généralement en entrée du graphique une entrée fictive symbolisant la lancée de l’opération et une sortie fictive symbolisant la livraison ou la fin de l’assemblage. Le graph ne doit pas contenir de contrainte non définie en amont (pas d’opération sur numéraire). On peut cependant ajouter des nœuds fictifs pour respecter la contrainte de monographie.
Quelques exemples illustratifs.
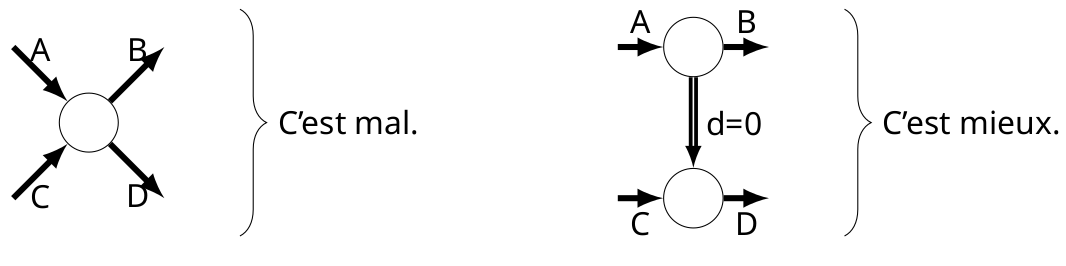
Pour illustrer un processus où B et D dépendent de A, mais où D dépend aussi de C, on ajoutera plutôt un nœud fictif.
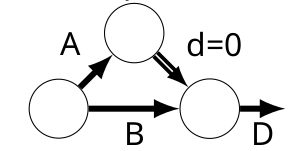
De la même manière pour les dépendances conjointes où D dépend de A et B.
On peut alors réáliser le diagramme de l’ensemble du processus avec ces quelques règles:
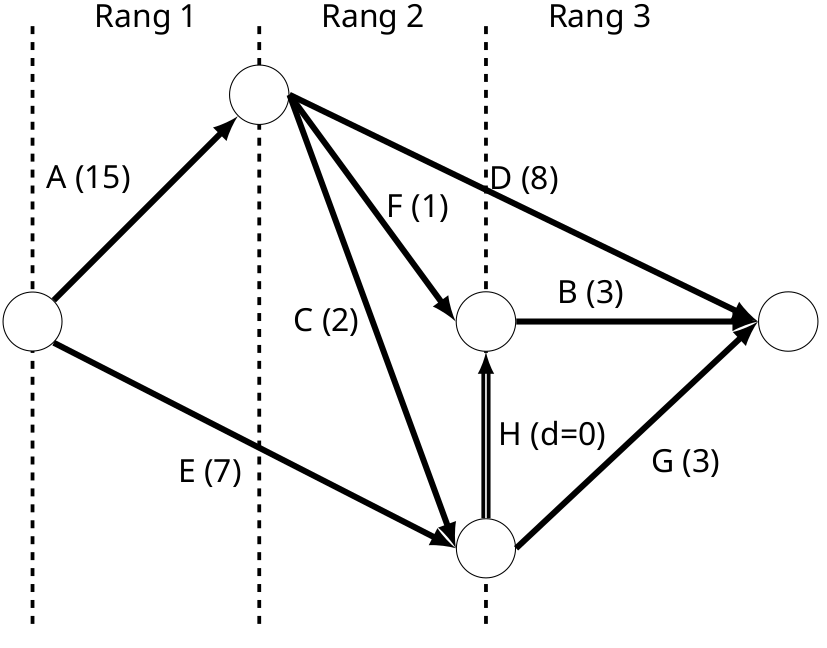
Diagramme de PERT final.
Calcul du chemin critique
On commence par calculer les date de réalisation au plus tôt. Avec le premier sommet avec une date à 0 (lancement au plus tôt), chaque sommet on prend la valeur maximum parmi les dates de réalisation au plus tôt des sommet précédents auxquels il est connecté, à laquelle s’ajoute la durée des étapes qui connecte les deux sommets.
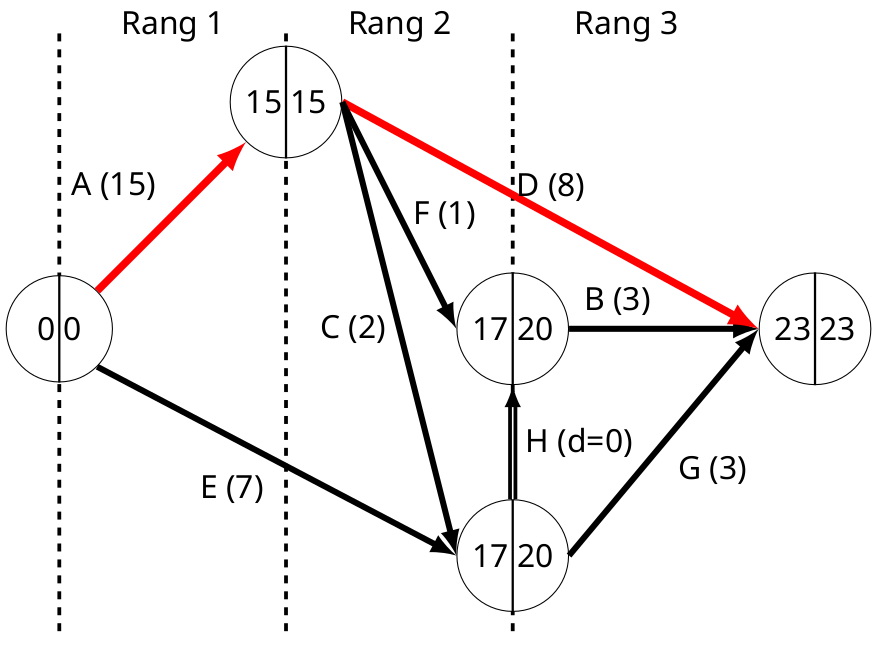
Diagramme de PERT avec les dates au plus tôt (gauche) et les dates au plus tard (droite). Le chemin critique est représenté en rouge plus épais.
Pour la date au plus tard on aura le raisonnement inverse en plaçant le dernier sommet à la date de livraison au plus tard. Le chemin critique est celui qui fixe la durée finale. Sa durée est incompressible, il n’existe pas de marge entre les tâches qui le constituent.
Comme pour le diagramme de Gantt, le diagramme de PERT est un outil de visualisation rapide. Il est important de le garder le plus clair possible et de ne pas le surcharger pour qu’il reste lisible sans trop d’effort. Par ailleurs, un diagramme de PERT ne dit rien sur la géographie de l’implémentation ou les autres contraintes. Il est donc important de le compléter avec d’autres informations car, seul, il n’est pas très utile.
Reste du cours: